JAVA 자료구조 (배열) 1 - 덧셈 하여 타깃을 만들 수 있는 배열의 두 숫자

풀이1 - 블루트 포스로 계산

 

그림 7-3 브루트 포스 풀이

 

위 문제에 대한 풀이를 한번 생각해 보자. 배열을 두 번 반복하면서 모든 조합을 더해서 일일이 확이해보는 무차별 대입 방식인 브루트 포스(Brute-Force)로 그림 7-3과 같은 방식을 떠올릴 수 있다.

 

이 그림에서는 정답을 찾기 위해 2부터 시작해 다른 엘리먼트들인 6,11,15를 차례대로 모두 비교한다. 즉 2 + 6,  2+ 11, 2+ 15와 같은 식으로 마지막 엘리먼트까지 모두 차례대로 더한 값을 비교해가며 정답을 찾을 때 까지 계속 진행한다. 이 방식이 바로 무차별 대입 방식인 브루트 포스로, 앞으로 문제를 풀 때 비효율적인 풀이법에서 꼭 한 번씩 첫 번째 풀이로 등장할 것이다.

public int [] solution(int [] nums ,int target) {
    for (int i = 0; i < nums.length; i++) {
        for (int j = i + 1; j < nums.length; j++) {
            if (nums[i] + nums[j] == target) {
                return new int[]{i, j};
            }
        }
    }
   
   return null;
}

 

위 경우 풀이 시간 복잡도는 O(n²)이다. 정확히는 1/2n² 정도가 되겠지만 시간의 복잡도를 표기할 때 상수 항은 기입하지 않기 때문에 n²이다. 문제가 풀리기는 하지만 브루트 포스 방식은 모두 탐색해야 하기 때문에 지나치게 비효율적이다. 

 

풀이2 - 첫 번째 수를 뺀 결과 키 조회

시간 복잡도를 개선해 속도를 높여보자. 비교나 탐색 대신 한 번에 정답을 찾을 수 있는 방법은 없을까?

public int[] solution(int[] nums, int target) {
    //키와 값을 바꿔서 맵으로 저장
    Map<Integer, Integer> numsMap = new HashMap<>();
    for (int i = 0; i < nums.length; i++) {
        numsMap.put(nums[i], i);
    }

    //target에서 첫 번째 수를 뺀 결과를 키로 조회하고 현재 인덱스가 아닌 경우 정답으로 리턴
    for (int i = 0; i < nums.length; i++) {
        if (numsMap.containsKey(target - nums[i]) && i != numsMap.get(target - nums[i]))
            return new int[]{i, numsMap.get(target - nums[i])};
    }
    
    //항상 정답이 존재 하므로 널이 리턴되는 경우는 없다.
    return  null;
}

 

일단 배열을 index와 value를 뒤집어서 map에 저장한다. 그리고 nums for문을로 돌려 다음에 충족하는 요소가 있는 지를 확인한다. ( target - i번째 요소 )에 충족하는 값이 있는지 containsKey()를 사용해서 numsMap을 검색한다. 충족하는 key-value가 있다는 것은 (i 번째 요소 + 충족하는 key-value의 key 값) 이 수식의 값이 target과 같다는 것이다. 하지만 충족하는 key-value의 value가 i번째 요소의 i와 일치하면 그것은 자기 자신이므로 이 둘이 같은지 확인하고, 같지 않다면 i 번째 요소의 index값과 충족하는 key-value의 value를 정답으로 return 한다. 

 

 

맵은 HashMap 자료형을 사용했고 자바에서 HashMap은 내부적으로는 해시 테이블로 구현되어 있다. 이 경우 조회는 평균적으로 O(1)에 가능하다. 최악의 경우에는 O(n)이 될 수 있지만 말 그대로 최악의 경우이고 드문 경우이므로 분할 상환 분석에 따른 시간 복잡도는 O(1)이며, 전제는 O(n)이 된다.

 

 

풀이3 -  조회 구조 개선

맵 저장과 조회를 2개의 for문으로 각각 처리했던 방식을 좀 더 개선해 이번에는 하나의 for로 합쳐서 처리해 보자 이 경우 전체를 다 맵에 저장할 필요 없이 정답을 찾으면 함수를 바로 빠져나올 수 있다. 동일한 O(n)에서 약간의 차이만 있을 뿐이라 풀이2와 비교해 성능상 큰 이점의 차이는 없다.

public int[] solution(int[] nums, int target) {
    //키와 값을 바꿔서 맵으로 저장
    Map<Integer, Integer> numsMap = new HashMap<>();
    //target에서 첫 번째 수를 뺀 결과를 키로 조회하고 현재 인덱스가 아닌 경우 정답으로 리턴
    for (int i = 0; i < nums.length; i++) {
        if (numsMap.containsKey(target - nums[i]) && i != numsMap.get(target - nums[i])) {
            return new int[]{numsMap.get(target - nums[i]),i };
        }
        //정답인 요소가 없으면 해당 index를 value로 요소를 key로 저장한다.
        numsMap.put(nums[i],i);
    }

    //항상 정답이 존재 하므로 널이 리턴되는 경우는 없다.
    return  null;
}

 

실행 속도를 확인해봐도 예상했던 것 처럼 풀이 #2와 큰 차이는 없지만 훨씬 더 빨르고 무엇보다 코드가 간결해 졌다. 정답을 반환 할때 {i, numsMap.get(target - nums[i])} 였던 것을  {i, numsMap.get(target - nums[i])} 바꾼 이유는 numsMap에 key-value를 넣는 것을 같은 for 문에서 돌리기 때문에 num[i]의 값이 6 일때 정답이 반환 되므로 맵에 들어 있는 값이 현재 인덱스 보다 항상 더 작으므로 풀이 #2와는 반대로 정답을 반환한다. 물론 정답이 [1, 0] 이든 [0, 1]이든 모두 정답으로 간주 되기 때문에 문제 풀이에 문제는 없지만 이와이면 작은 값부터 차례대로 리턴되도록 맵에 있는 값을 먼저 리턴했다.

 

풀이4 - 투 포인터 이용

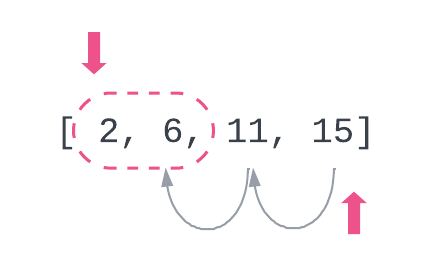
이 문제를 투 포인터로 풀 수 있을 까? 투 포인터란 왼쪽 포인터와 오른쪽 포인터의 합이 타깃보다 크다면 오른쪽 포인터를 왼쪽으로, 작다면 왼쪽 포인터를 오른쪽으로 옮기면서 값을 조정하는 방식이다. 이런 방식으로 그림 7-4와 같이 타깃에 일치하는 2개의 포인터를 찾아나간다.

 

위 그림에서 타깃인 8를 찾기 위한 양쪽 포인터의 합은 맨 처음 에는 각각 2와 15에 위치했기 때문에 17이었다. 이때 합의 값이 8보다 크기 때문에 오른쪽 포인터는 한 칸씩 왼쪽으로 이동해싿.  그리고 6에 이를러서 2 + 6 = 8인 정답 위치 0, 1을 찾을 수 있었다.

 

public int[] solution(int[] nums, int target) {
   int left = 0;
   int right = nums.length - 1;

   while (left != right){
       int item = nums[left] + nums[right];
       if(item > target) {
           right -=1;
       } else if (item < target ) {
           left +=1;
       }else {
           return new int[]{left, right};
       }
       
   }

    //항상 정답이 존재 하므로 널이 리턴되는 경우는 없다.
    return  null;
}

 

코드로 구현 하면 위와 같다. 투 포인터로 구현해보니 코드도 간결하고 이해하기 쉽다. 투 포인터의 시간 복잡도도 O(n)이고, 불필요한 추가 계산도 필요 없으면, 매우 빠른 속도가 기대 된다. 그러나 이 문제는 투 포인터로 풀 수 없다. 왜냐하면 투 포인터는 주로 정렬된 입력값을 대상으로 하며, nums는 정렬된 상태가 아니기 때문이다. 다음과 같이 정렬 로직을 추가해 보자

 

public int [] solution(int[] nums, int target){
    Array.sort(nums);
    ...
}

 

그런데 이렇게 하면 인덱스가 모두 엉망이 되기 때문에 심각한 문제가 발생한다. 만약 이 문제가 인덱스가 아니라 값을 찾아야 하는 문제라면, 얼마든지 정렬하고 투 포인터로 풀이할 수 있다. 하지만 이처럼 인덱스를 찾아내는 무넺에서는 이렇게 정렬을 통해 인덱스를 섞어 버리면 곤란한다. 원래 인덱스를 찾을 수 없기 때문이다.

 

풀이	방식	실행 시간
1	브루트 포스로 계산	90밀리초
2	첫 번째 수를 뺀 결과 키 조회	11밀리초
3	조회 구조 개선	6밀리초
4	투 포인터 이용	풀이 불가

 

 

 

[출처 - 자바 알고리즘 인터뷰 with 코틀린 , 저 박상길]

https://www.onlybook.co.kr/entry/java-algorithm-interview