자료구조 - 트리,이진 검색트리(BST)

1. Tree 소개 

1.1. Tree자료구조란 무엇일까? 

tree는 linked list처럼 노드로 이루어진 데이터 구조이다. 그렇지만 노드들 사이에 부모-자식 관계가 있다. 결과적으로 가지(branch)를 가지게된다. 그러니까 한 노드는 다른 노드로 연결되어 있는데 2개나 3개 10개 아니면 0개가 될 수도 있다. 그렇게 되면 노드가 branch를 가지는 구조가 되는데, 그래서 이름을 tree라고 한다.

 

가지를 따라가면 어느 지점에서 나뉘게 되고, 그 가지는 계속해서 나뉠 수 있다. 그러면 원래 줄기에서 뻗어나온 수많은 작은 가지들이 남게된다.보통 다이어그램을 보게되면 root노드를 기준으로 위에서 아래로 내려오는 경우가 많다. 

 

 

list는 선형구조이다. 한가지가 있고, 그 다음에 하나, 그다음에 하나 그런식으로 모든 것이 한 줄로 늘어서 있다. 트리는 비선형 구조이다. 한 갈래 말고도 여러 가지들을 뻗을 수 있다. linked list에서는 한 갈래로만 뻗어간다. 이중 연결 리스트에서는 앞뒤로 작업이가능하다. 그렇지만 여전히 데이터 구조 속에는 한 갈래의 길 밖에 없다. 트리에서는 갈 수 있는 경로가 여러 갈래이다. 

 

1.2. Tree가 아닌 경우 

1.2.1. 형제 레벨의 노드를 가르키고 있는 경우

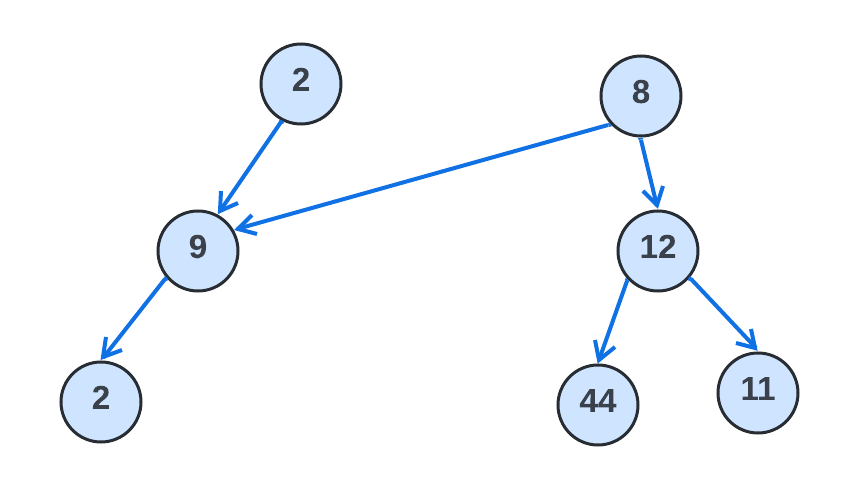
위 그림은 tree자료구조가 아니다. 위 그림을보면 데이터 값으로 9,8을 가지고 있는 노드들이 자신보다 더 낮은 곳에 있지 않은 다른 노드를 가리키고있다. 자식레벨의 노드가 아닌 노드를 가르키고 있는 것이다. tree자료 구조의 경우 노드는 부모-자식 관계에 따라서 자식 노드만을 가리킬 수 있다. 자식이 부모 노드를 가르키고 있다거나 특정 노드가 자신의 형제 레벨의 노드를 가르키고 있으면 안된다. 위와 같은 모양의 자료구조는 그래프(graph)이다. 트리에서는 모든 노드가 루트에서 멀어지는 방식으로 연결된다. 다음 노드를 가르키고 있는 화살표가 모두 아래쪽을 향하고 있어야 한다.

 

1.2.2. 루트가 하나가 아닌 경우 

 

모든 노드가 루트에서 멀어지는 방향을 가르키고 있으므로 트리인 것처럼 보이지만, 루트가 하나가 아니다. 위 그림의 루트는 출발점이 두 개이다. 그러니까 트리가 아니다. 출발지점이자 tree의 루트는 하나여야 한다. 

 

1.3. Tree 용어 정리

• Root - tree의 제일 꼭데기위 위치하는 노드 
• Child - 루트에서 멀어지는 방향으로 연결된 노드 
• Parent - 자식의 반대 개념이다. 
• Siblings - 같은 부모를 가지는 노드를 의미한다.
• Leaf - 자식이 없는 노드를 의미한다. 
• Edge(간선) - 한 노드에서 다른 노드로 향하는 화살표이다.

---

2. Tree 사용

2.1. Tree가 실제로 사용되는 예시

• HTML DOM
• 네트워크 라우팅 
  • https://ko.wikipedia.org/wiki/%EB%9D%BC%EC%9A%B0%ED%8C%85
• 추상화 트리(Abstract Syntac Tree)
• 운영체제에서 폴더가 설계된 방식 

 

---

3. 이진트리(Bnary trees) 소개

3.1. Tree의 종류

• Tree
• Binary Trees(이진트리)
• Binary Search Trees(이진 검색 트리)

 

이름에서 알수 있듯이 이진 탐색트리는 탐색(search)에 강점을 보인다. 정렬된 데이터를 특정한 방식으로 저장한다. 

 

3.2 이진트리(Binary Trees)의 기본 조건

이진 트리는 각 노드가 최대 두 개의 자식을 가져야 한다는 특별한 조건이 있다. 그러니까 이진트리의 경우는 자식이 1)0개이거나, 2)1개이거나, 3)2개일 수 있다. 보통 루트 노드는 두 개의 자식 노드를 가지는데, 그 각각이 다시 한개, 0개, 2개의 자식을 가진다. 

 

이진트리의 경우 순회가 쉽다는 장점이 있기 때문에 자주 사용된다. 이진탐색트리를 다루게 되면서 본격적으로 알게되겠지만, 이진 탐색 트리는 이진 트리의 특별한 종류이고, 이진 트리는 다시 트리의 한 종류가 된다. 그리고 이진탐색 트리는 특별한 방식으로 정렬되어 있다. 데이터가 순서에 따라 저장되어있다. 

 

3.3 이진 검색 트리(BST:Binary Seach Trees)

이진 탐색 트리즉 BST 이진트리의 특별한 종류이고, 이진 트리는 다시 트리의 한 종류이다. 이진트리와 BST 모두 최대 노드당 두 개의 자식을 가진다. 0, 1, 2개의 자식이다. 

 

그리고 BST는 특별한 방식으로 정렬이 되어있다. 데이터가 순서에 따라 저장되어 있다. 왜냐하면 BST는 데이터를 비교해서 정렬가능하게 저장하기 때문이다. 일반적으로는 숫자를 다루는데, 사실 어떤 데이터를 대상으로 작업을 하든 크게 상관은 없다. string 타입이 저장될 수도 있고 다른 종류의 데이터가 저장될 수도 있다. 하지만 그런 데이터들을 비교하고 순서를 매기는 정렬기준이 있어야한다. 이것이 BST가 작동하는 방식이다. 

 

위 그림의 BST는 노드 보다 작은 숫자를 데이터를 가진 노드는 왼쪽에 위치하게 되어 있다. 노드보다 큰 숫자 데이터를 가진 노드는 오른쪽에 위치하게 되어있다. 이건 각 자식 노드에 대해 반복된다. 

 

3.4 BST가 작동하는 방식

• 모든 부모 노드는 최대 2개의 자식노드를 가진다. 
• 모든 부모 노드의 왼쪽 노드는 언제나 자식노드 보다 작다.
• 모든 부모 노드 오른쪽에 있는 자식노드는 언제나 자식노드 보다 크다.

 

위 그림의 BST를 살펴보면 BTS 루트를 기준으로 루트 왼족에 있는 노드의 값들은 모두 41보다 작다. 반면 루트 오른쪽에 있는 노드들의 값은 41보다 크다. 그다음 값 20을 가지고 있는 노드로 내려와도 해당 노드를 기준으로 왼쪽에 있는 노드들은 모두 20보다 값이 작은데 오른쪽에 있는 노드의 값은 20보다 크다.

 

이러한 점이 이진 탐색트리(BST)에 특성이고, 그냥 이진 트리와 다르게 해주는 점이다. 데이터가 특정한 순서로 저장되는 것이다. 모든 노드에 대해 부모 노드보다 오른쪽에 있는 자식 노드는 부모노드보다 크고 왼쪽에 있는 노드는 부모노드보다 작다. 

 

3.5 BST가 사용되는 이유

bst 실제로 정렬되는 순서, 그러니까 부모보다 큰 것들은 오른쪽에 작은 것들은 왼쪽에 놓는 방식은 무언가 원하는 요소를 찾는 것을 아주 빠르고 쉽게 만들어준다. 그리고 새로운 요소를 추가하는 것과 새로운 요소(노드)의 자리를 찾는 것도 쉽게 해준다. 그렇기 때문에 이진 탐색 트리에서 무언가를 찾는 것은 정렬되지 않은 트리와 비교하면 아주 빠르다. 

 

작동방식 예시

위 그림의 트리에서 72를 찾는 다고 생각해 보자. 72라는 값을 가진 노드를 찾기는 여정을 시작하는 곳은 언제나 트리의 루트가 된다. 위 그림 상에 어떤 노드에 어떤 값이 있는지 훤히 알 수 있는 상황과는 다르게 코드상에서는 41값에 해당하는 루트 노드에 있을때는 실제로 앞을 볼수 없어서 하위 자식 노드에 어떤 값들이 있는지 알수 없다.  

 

그러므로 첫번째 할일은 확인을 하는 것이다. 1) 72는 41보다 큰가? true -> 41 우측에 있는 노드들만 살펴본다. 따라서 기본적으로는 매번 특정 위치의 노드에서 비교를 할때 마다 우리가 봐야하는 숫자의 값이 대략 반으로 줄어 들게 되는 것이다. 이진 탐색이 리스트에서 어떻게 작동했는지를 기억한다면, 기본적으로 이것도 같은 개념이다. 부모 노드보다 더 큰것은 모두 오른쪽에, 더 작은 것은 왼쪽에 두자는 것이다. 

 

비교후에 비교대상의 값이 얼마나 줄어 들었느냐는 트리가 어떻게 구성되어 있는지에 따라 다르다. 루트 노드를 기점으로 오른쪽에는 더 많은 값이 있고 왼쪽에는 더 적은 값이 있을 수도 있다. 그렇지만 일반적으로, 비교하는 횟수나 노드의 숫자가 절반으로 준다고 보면 된다. 

 

 

2) 72는 65보다 큰가? ture -> 우측에 있는 노드들만 살펴본다. 그 다음으로 만나게 되는 노드의 값은 91이다. 3) 72는 91보다 큰가? false? 좌측에 있는 노드들만 살펴본다.  그 다음에 만나게 되는 노드의 값은 72로 원하는 노드의 값을 찾았다. 

 

 

만약 이게 정렬되지 않은 트리이고 72가 그 안에 있는 경우와 비교해 보자. 그렇다면 72는 트리 전체 아무 곳에나 있을 수 있다. 그러면 우리는 모든 노드를 확인하면서 트리 전체를 순회하여야 한다.  하지만 그렇다면 어떤 기준으로 트리를 살펴볼지 기준이 모호해진고 아마 트리를 훑어 보는 방식에 대한 굉장히 많은 경우의 수가 나올것이다. 

 

그러나 bst(이진 탐색 트리)에서는 값을 찾을 때 사용하는 특정한 과정이 있다. 비교해서 왼쪽이나 오른쪽을 결정하는 것이다. 

그리고 다시 비교를 해서 반으로 트리를 쪼개는 것이다. 이런 작없을 해당 값을 찾거나 못 찾을 때까지 반복한다. 그렇지만 알다시피, 이진 탐색 크리가 작동하는 방식에 따라서 검색했는데 해당하는 값을 찾지 못한다면 트리 안에 찾고자 하는 값이 없는 것이다. 

 

 

[출처 - JavaScript 알고리즘 & 자료구조 마스터클래스 - 저, ColtSteele]

https://www.udemy.com/course/best-javascript-data-structures